This is the follow-up to last week’s the easiest win in options is for stock traders. In that post, we started with a puzzle that leads to a critical insight: The collective pursuit of option arbitrage means that we can use put-call parity in reverse — to imply the cost of carry instead of assuming one, … Continue reading implying the cost of carry in options→ The post implying the cost of carry in options appeared first on Party at the Moontower.| Party at the Moontower
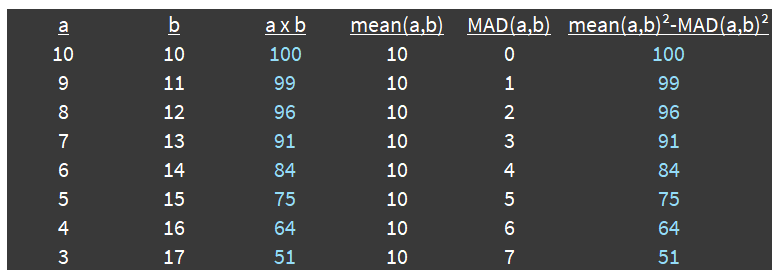
I used a pattern to explain it to my 12-year-old on our car ride on Monday. Start with: 8*8 = 64 Let’s call that a * b It feels like if we subtract 1 from a and add 1 to b multipy it should be close to 64 7*9 = 63 Close but a tad lower. What if we keep … Continue reading how I explained vol drag to a 12-year-old →| Party at the Moontower
Notable short seller Andrew Left’s firm Citron Research gave his “all roads lead to $40” pronouncement on X this week regarding PLTR 2.90%↑ : Created with TradingView Give Palantir the same $100 billion valuation that Databricks just earned. Where does that put the stock? $40. The exact same math we saw when comparing Palantir to OpenAI. Tyler pinged me before the stock dove … Continue reading Betting on PLTR to $40 →| Party at the Moontower
A conversation with Claude Opus 4 KA: What is the compact formula for daily option pl that relates realized variance – implied variance? The compact formula for daily option P&L that relates realized variance to implied variance is: Daily P&L ≈ ½ × Vega × (σ²_realized – σ²_implied) × Δt Where: Vega = option’s vega … Continue reading Sparring with AI: Theoretical options p/l vs discrete hedging →| Party at the Moontower
