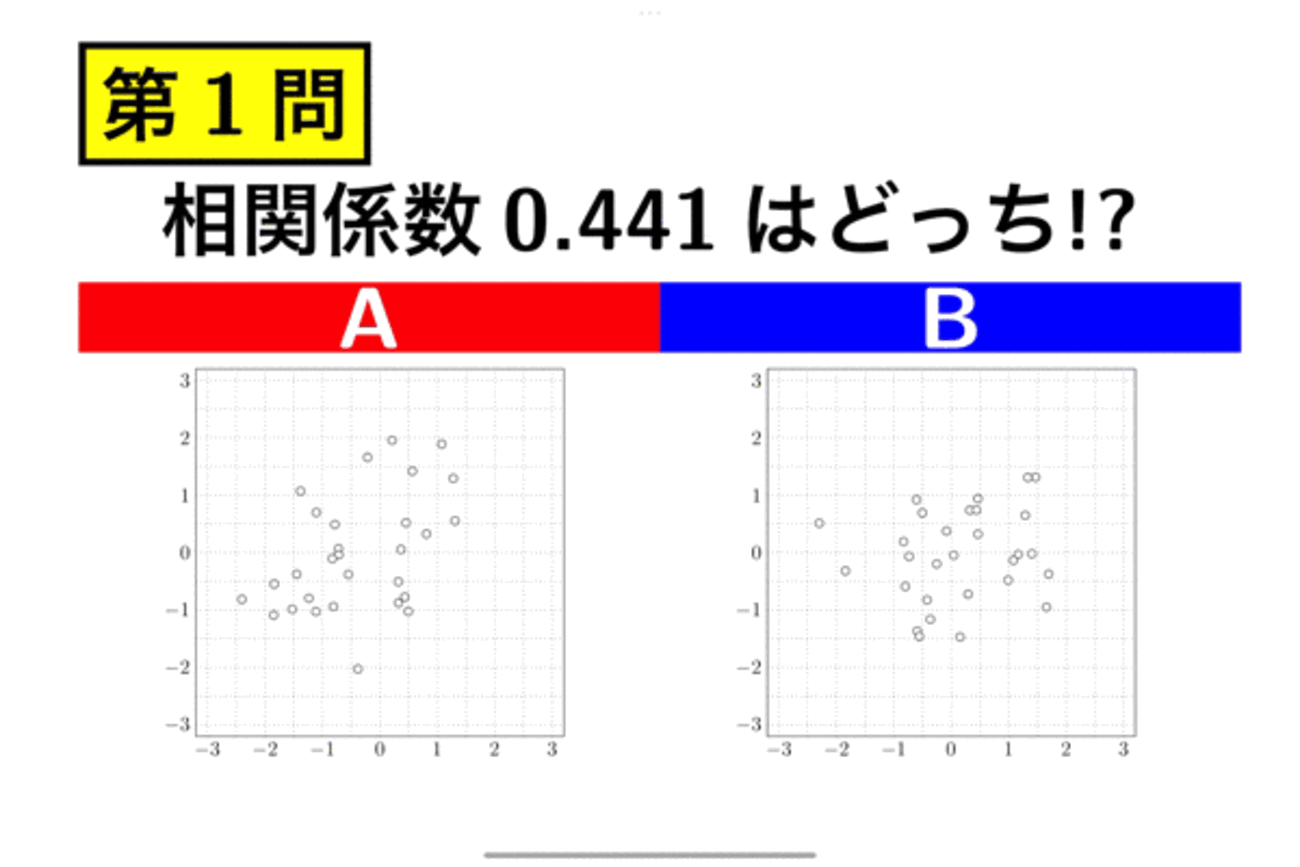
この記事は TeX & LaTeX Advent Calendar 2023 の18日目の記事です。17日目はYarakashi_Kikohshiさんでした。 19日目は7danmoroboshiさんです。 【目次】 大学入学共通テストの新傾向問題と言えば……!? 検討ポイント 乱数生成アルゴリズムの選択 「指定された相関係数を持つ2つの乱数列」をいかにして生成するか? 定理 証明 注意:生成した乱数列の相関係数は再測定が必要 相関係数格...| TeX Alchemist Online
可算選択公理を仮定しない構成的数学では、Cauchy列に基づいた実数の構成をやるときに完備性が示せなくなる(らしい)。この弱点は、実数の構成に使うCauchy列を有理数の点列ではなく、有理数の集合の列とすれば克服できる。| 雑記帳
「集合\(A\)が有限集合であるとは、ある自然数\(n\)に対し、\(A\)と\(\{0,1,\dotsc,n-1\}\)の間に全単射が存在することである。一方、有限集合ではない集合は無限集合である。」| 雑記帳
構成的数学に基づいて解析学を展開し、プログラミングでそれを実装するようなコンテンツを作れないかなあと去年ぐらいから考えています。| 雑記帳
ランキング参加中その他たびたび見かける疑問として,「一階述語論理のストラクチャー(構造)の対象領域を空にしてはなぜダメなのか?」というものがある.これ自体はとても良い質問なのだが,「わかる人(つまり教科書を書くような人)にはすぐわかるが,初学者にはすぐわからない」という難易度の問題のため,初学者が目を通すような教科書などに答えが...| Sokratesさんの備忘録ないし雑記帳
伝統的な数学のゼミは,河東先生のホームページ How to prepare for seminars に書いてあるような「予習してきた人が参加者全員の前で発表する」という方式を取る*1.このやり方は少なくとも数学専攻の学生向けが自分の専門としたい領域を学習する方法として最適であろうと言われているし,私自身もそう思っている. 一方で,この方法は予習の負担が明らかに大きい.そ...| Sokratesさんの備忘録ないし雑記帳
数学は哲学?特におもしろくもない冗談を言うのはよせよ.| Sokratesさんの備忘録ないし雑記帳
ランキング参加中その他環の公理から \( (-m)\times (-n) = m \times n \) を証明する.自分用のメモを公開しているというノリなので,説明が不十分な箇所があるかもしれないが,追記するかも知れないし,しないかも知れない. 環の公理 いくつかの補題 (マイナス)✕(マイナス)=(プラス) 関連文献| Sokratesさんの備忘録ないし雑記帳
同じように自然数のペア全体の集合を適切な同値関係で割ることで整数全体の集合を構成してみよう(練習問題)— そくらてす (@7danmoroboshi) 2023年2月20日 という問題を出したので,それの想定回答をここに記す. \(\newcommand{\mathnat}{\mathbb{N}}\) \(\newcommand{\mathint}{\mathbb{Z}}\) \(\newcommand{\mathpair}[2]{(#1, #2)}\) 問題 想定回答 想定回答の直観 別解の概略 参考文献 関連記事 問題 \((\math...| Sokratesさんの備忘録ないし雑記帳
むしゃくしゃしたので,数学での「公理(Axiom)」について語ろうと思う.雑多な文章の寄せ集めで,特にオチがあるわけではないので,そういうのが苦手な人は回れ右して帰ると良い. 「公理」の2つの用法 「公理」に正しさ? 公理と対象の存在 どのような命題を「公理」とするか 総括 参考文献 関連記事| Sokratesさんの備忘録ないし雑記帳
\(\newcommand{\mathreal}{\mathbb{R}}\) \(z^{2}=i\) という少し思い入れのある方程式を解く. \(z^{2}=i\) の思い出 \(z^{2}=i\) の解法 その1 \(z^{2}=i\) の解法 その2 おわりに 参考になるかもしれない文献 \(z^{2}=i\) の思い出 まだ,私が高校生だった頃,虚数 \(i\) が導入されたときは驚いた.\(x^{2}=-1\) を解けるように「数」が拡張されたからである. このとき, 同じように二乗したら \(i...| Sokratesさんの備忘録ないし雑記帳
定理 $n \times n$ 正定値実対称行列 $A,B$ に対して,次の不等式が成り立つ. \[ \det(A+B)^{1/n} \geq \det A^{1/n} + \det B ^{1/n} \]以下の行列式の特徴づけから従う.補題 $n\times n$ 正定値実対称行列 $M $ に対し,次の等式が成り立つ. \[ \inf_{X \succ O: \det X = 1} \mathrm{tr}(MX) = n \det M^{1/n} \] ここで, $X \succ O$ は $X$ が正定値実対称行列という意味である.これを認めれば, \[ \begin{align} n …| むしゃくしゃしてやった,今は反省している日記
数理最適化 Advent Calendar 2020 20日目の記事です.昨日はyappy0625さんの『天体ショーを整数計画問題で解いてみた。』,明日はshuhei_fさんのSVMの話です.今回紹介するのはBlackwellの接近可能性定理という定理です.一言でいうと,von Neumannのミニマックス定理の拡張なのですが,オンライン最適化(リグレット最小化)と深いつながりがあります.最近研究で使って非常に面...| むしゃくしゃしてやった,今は反省している日記
この記事は Mathematical Logic Advent Calendar 2023 - Adventar と Math Advent Calendar 2023 - Adventar の16日目の記事である.より正確にはMathematical Logic Advent Calendar 2023 - Adventarの主催に書くことを強要された記事である. adventar.org ←昨日 Robustly Isomorphic Models | Mathlog →明日 空白 adventar.org ←昨日 エブリシング・エブリウェア・オール・アット・ワンス・関数 - 電波通信 →…| Sokratesさんの備忘録ないし雑記帳
NHK で放映された『笑わない数学』という番組の次の回が話題になっていた. www.nhk.jp 企画意図としては「\(1+1=2\) という式を通して数学基礎論という分野を紹介する」というものだったのだが,怪しい説明や誤解を招く説明,端的に誤っている説明があった.というか,全体を通してそういうものがとても多かった.どう少なく見積もっても番組の内容の半分以上がそう...| Sokratesさんの備忘録ないし雑記帳
NHK で放映された『笑わない数学』という番組の次の回が話題になっている. www.nhk.jp 企画意図としては「\(1+1=2\) という式を通して数学基礎論という分野を紹介する」というものだったのだが,いくつか怪しい説明や誤解を招く説明,端的に誤っている説明が散見された.というか,全体を通してそういうものがとても多かった.どう少なく見積もっても番組の内容の半...| Sokratesさんの備忘録ないし雑記帳
論理学とその周辺領域の本を並べてみた*1.この記事にあげる本は,何らかの形でわたし自身が手に取ったことのあるもの(読んだとは言っていない)に限定している*2.ただし,原語版は手に取ったことがあるが,日本語訳はそうではない,またはその逆という場合はある. すべての本に対してコメントをしきれていないので,周りからサボりを指摘されやすいように,...| Sokratesさんの備忘録ないし雑記帳
条件を満たすものが何通りあるか数える問題、すなわち数え上げ問題には様々なものがありますが、「\(n\) 個の玉を \(x\) 個の箱に分ける方法は何通りか」などといった、典型的な...| アルゴリズムロジック
以下の2つを混同しそうですが、ここでは \(p_{\leq k}(n)\) を求めることを考えます。 \(p_k(n)\) : 自然数 \(n\) を \(k\) 個の 1 以上...| アルゴリズムロジック
以下の2つを混同しそうですが、ここでは \(p_k(n)\) を求めることを考えます。 \(p_k(n)\) : 自然数 \(n\) を \(k\) 個の 1 以上の整数に分割す...| アルゴリズムロジック
ベル数は「写像12相」と呼ばれるものを通して学ぶと、他の数え上げ問題との関わりが分かり全体像がスッキリします。ぜひ確認してみることをおすすめします。「写像12相」で典型的な数え上...| アルゴリズムロジック
第2種スターリング数は「写像12相」と呼ばれるものを通して学ぶと、他の数え上げ問題との関わりが分かり全体像がスッキリします。ぜひ確認してみることをおすすめします。「写像12相」で...| アルゴリズムロジック
一个违反直觉的概率问题| frostming.com